Quick Sort
The quick sort runs faster because it is efficient, and it runs in-place (unlike the merge sort).
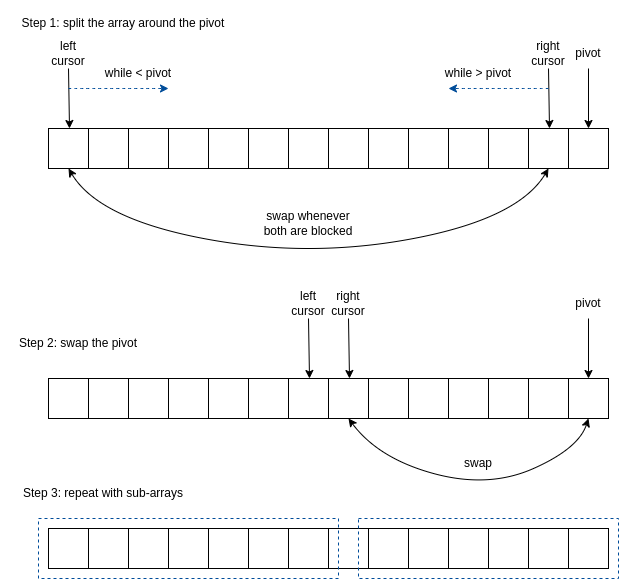
It works by:
- choosing a value to be the “pivot” point.
- In the remaining array, it swaps values between left and right cursors until
- all values up to and including the left cursor are less than the pivot.
- all values on or after the right cursor are greater than or equal to the pivot.
- Then the pivot is swapped into the middle, trading places with the right pivot.
- The process gets repeated on the sub-arrays to the right and left of the pivot.
The quick sort is:
- not stable, equal values may be swapped. This can be worked around by adjusting your comparison logic.
- in-place, it uses no significant amount of extra memory.
- Efficient, having O(n * log(n)) performance.
- possible to parallelize. At step 3 in the diagram, separate coroutines or threads could be created if the sub-arrays are still quite large.
- works with non-numerical types, it uses a comparator.
The quick sort algorithm was made to handle sorting large arrays, but in practice, the merge sort algorithm tends to be used for larger arrays instead.
Since the quick sort uses recursion, it is possible to have a stack overflow in your program, unless the program is written to work around recursion.
Example In Golang
package srt
func quickSort(nums []int, start int, stop int) {
// pivot from right
if start >= stop {
return
}
mid := partition(nums, start, stop)
if mid > start+1 {
quickSort(nums, start, mid-1)
}
if mid < stop-1 {
quickSort(nums, start+1, stop)
}
}
func partition(nums []int, start, stop int) int {
if stop <= start {
return -1
}
pivotIndex := stop
pivot := nums[pivotIndex]
j := start - 1
for i := start; i < pivotIndex; i++ {
if nums[i] < pivot {
j++
nums[i], nums[j] = nums[j], nums[i]
}
}
j++
nums[pivotIndex], nums[j] = nums[j], nums[pivotIndex]
return j
}
func quickSort(nums []int, start int, stop int) {
// pivot from right
if start >= stop {
return
}
mid := partition(nums, start, stop)
if mid > start+1 {
quickSort(nums, start, mid-1)
}
if mid < stop-1 {
quickSort(nums, start+1, stop)
}
}
func partition(nums []int, start, stop int) int {
if stop <= start {
return -1
}
pivotIndex := stop
pivot := nums[pivotIndex]
j := start - 1
for i := start; i < pivotIndex; i++ {
if nums[i] < pivot {
j++
nums[i], nums[j] = nums[j], nums[i]
}
}
j++
nums[pivotIndex], nums[j] = nums[j], nums[pivotIndex]
return j
}
Python Example
def shift(ar, from_index, to_index):
i = from_index
v = ar[from_index]
while i < to_index:
ar[i] = ar[i+1]
i += 1
ar[to_index] = v
def quick_sort(ar, from_index, to_index):
if to_index - from_index < 1:
return
pivot_index = to_index
pivot = ar[pivot_index]
index = from_index
while index < pivot_index:
if ar[index] > pivot:
shift(ar, index, pivot_index)
pivot_index -= 1
else:
index += 1
quick_sort(ar, from_index, pivot_index - 1)
quick_sort(ar, pivot_index+1, to_index)
if __name__ == "__main__":
inputs = [5,2,9,6,31,28,63,19,11,64,23]
quick_sort(inputs, 0, len(inputs)-1)
print(inputs)